Answer:
Second option: One solution. Independent.
Explanation:
The equation of the line in Slope-Intercept form is:

Where "m" is the slope and "b" is the y-intercept.
Since the equations of the system have this form, we know that they are lines.
We can identify that the y-intercept of the first equation
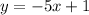 is:
is:
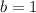
Now we need to find the x-intercept. Substitute
 and solve for "x":
and solve for "x":
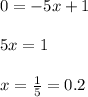
Then, we can graph the first line which passess through the points (0,1) and (0.2,0). Observe the graph attached.
The y-intercept of the second equation
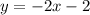 is:
is:
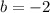
Now we need to find the x-intercept. Substitute
 and solve for "x":
and solve for "x":
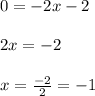
Then, we can graph the second line, which passess through the points (0,-2) and (-1,0).
You can observe in the graph that the lines intersect at the point (1,-4). Therefore, that point is the solution of the system of equations.
Since the lines intersect, then there is one solution that is true for both equations. It is independent