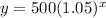Question

The value of a collector’s item is expected to increase exponentially each year. the item is purchased for $500. after 2 years, the item is worth $551.25. which equation represents y, the value of the item after x years? y = 500(0.05)x y = 500(1.05)x y = 500(0.1025)x y = 500(1.1025)x

Answer 1

`y=500(1.05)^x`

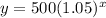
Explanation:

The standard form for an exponential equation is

`y=a(b)^x`

We have 2 unknowns, a and b, but that's all good because we have 2 (x, y) coordinates we can utilize in order to find a and b. In our coordinate pair, x is the number of years gone by and y is the value after that number of years. The problem tells us that an item was purchased for $500. That translates to "before any time has gone by, the initial value of the item is $500". In other words, with x being time, no time has gone by, so x = 0. When x = 0, y = 500. (0, 500). Do the same for the next set of numbers. When x = 2 years gone by, the value is $551.25, so the coordinate is (2, 551.25). Now we use them to find a. Use the first coordinate:

`500=a(b)^0`

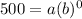
Anything raised to the 0 power = 1, therefore:

`500 = a(1)` and a = 500.

Now onto the next coordinate point using the a value we just found:

`551.25 = 500(b)^2`

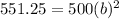
Divide both sides by 500 to get

`1.1025=b^2`

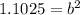
so b = 1.05.

Now we have the values for a and b, so we fill in:

`y = 500(1.05)^x`