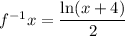Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).

Consider the given function.

pic below

Answer 1

• To determine the inverse of the given function,

Change f(x) to y , switch x and y , and solve for y.

• The resulting function may be written as:

`f^(-1)x=(\ln (x+4))/(2)`

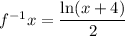
Explanation:

We know that while finding the inverse of a function the following steps are to be followed:

• We first put f(x)=y

• Then we interchange x and y in the expression.

• and then we finally solve for y.

We are given a function f(x) by:

`f(x)=e^(2x)-4`

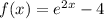
Now, we put

`f(x)=y`

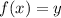
i.e.

`e^(2x)-4=y`

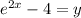
Now, we interchange x and y as follows:

`e^(2y)-4=x`

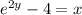
and finally we solve for y

i.e.

`e^(2y)=x+4`

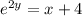
Taking logarithmic function both the side of the equation we get:

`2y=\ln (x+4)\\\\i.e.\\\\y=(\ln (x+4))/(2)`

i.e.

`f^(-1)x=(\ln (x+4))/(2)`