Question

A spring has a natural length of 8 m. If a 12-N force is required to keep it stretched to a length of 10 m, how much work W is required to stretch it from 8 m to 16 m? (Round your answer to two decimal places.)

Answer 1

The work is required to stretch it from 8 m to 16 m is 192 N-m

Step-by-step explanation:

Given that,

Natural length = 8 m

Force F = 12 N

After stretched,

length = 10 m

We need to calculate the elongation

`x = 10-8=2\ m`

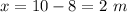
Using hook's law

The restoring force is directly proportional to the displacement.

`F\propto (-x)`

`F = -kx`

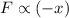
Where, k = spring constant

Negative sign shows the displacement in opposite direction

Now, The value of k is

`k = (F)/(x)`

`k = (12)/(2)`

`k = 6`

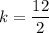
When stretch the string from 8 m to 16 m.

Then the elongation is

`x=16-8=8\ m`

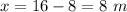
Now, The work is required to stretch it from 8 m to 16 m

`W = (1)/(2)kx^2`

Where, k = spring constant

x = elongation

`W=(1)/(2)*6*8*8`

`W=192\ N-m`

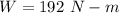
Hence, The work is required to stretch it from 8 m to 16 m is 192 N-m