Simplify the expression. the quantity x to the one fifteenth power end quantity to the power of 5

Question

asked Jul 9, 2020 60.2k views

2 Answers

Birjolaxew · Answer 1 · 2020-07-10T13:35:17+0000

Answer:

$\sqrt[3]{x}$ .

Explanation:

We have been given an expression
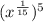$(x^{(1)/(15)})^5$ . We are asked to simplify our given expression.

We will use power rule of exponents
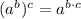$(a^b)^c=a^(b\cdot c)$ to simplify our given expression as:

$(x^{(1)/(15)})^5=x^{(1)/(15)* 5}$

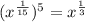
$(x^{(1)/(15)})^5=x^{(1)/(3)* 1}$

$(x^{(1)/(15)})^5=x^{(1)/(3)}$

Using fractional exponent rule
$a^{(1)/(n)}=\sqrt[n]{a}$ , we can write our expression as:

$(x^{(1)/(15)})^5=\sqrt[3]{x}$

Therefore, the simplified form of our given expression would be
$\sqrt[3]{x}$ .