Question

A car, originally valued at 70,000 in 2006 depreciates exponentially at a rate of 4% each year. Round the expected value of the car in 2018 to the nearest dollar. Round the expeated value of the car in 2018 to the nearest dollar

Answer 1

$42,890

Explanation:

The standard form for an exponential equation is

`y=a(b)^x`

where a is the initial amount value and b is the growth rate or decay rate and t is the time in years. Since we are dealing with money amounts AND this is a decay problem, we can rewrite accordingly:

`A(t)=a(1-r)^t`

where A(t) is the amount after the depreciation occurs, r is the interest rate in decimal form, and t is the time in years. We know the initial amount (70,000) and the interest rate (.04), but we need to figure out what t is. If the car was bought in 2006 and we want its value in 2018, a total o 12 years has gone by. Therefore, our equation becomes:

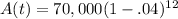`A(t)=70,000(1-.04)^(12)` or, after some simplification:

`A(t)=70,000(.96)^(12)`

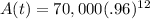
First rais .96 to the 12th power to get

A(t) = 70,000(.6127097573)

and then multiply.

A(t) = $42,890