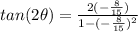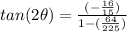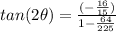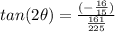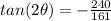Answer:
Part A)
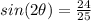
Part B)
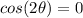
Part C)
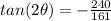
Explanation:
Part A) we have
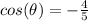
θ is in quadrant 3 ----> the sine is negative
Find
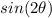
we know that
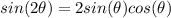
Remember that
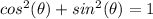
substitute
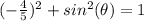
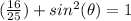
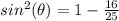
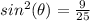
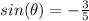 ---> remember that the sine is negative (3 quadrant)
---> remember that the sine is negative (3 quadrant)
Find
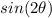
we have
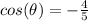
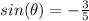
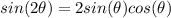
substitute
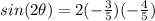
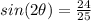
Part B) we have
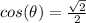
θ is in quadrant 1
Find
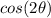
we know that
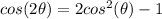
substitute
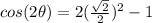
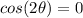
Part C) we have
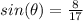
θ is in quadrant 2 ----> the cosine is negative
Find
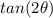
we know that
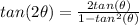
Remember that
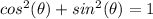
substitute
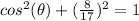
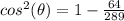
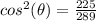
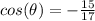
Find
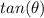
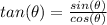
substitute
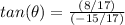
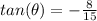
Find
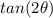
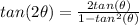
substitute