Question

A plot of land has an area 33.75 square feet. Jackson wants to put a 4-foot by 4 foot shed on the land. He can only do this if the height of the trapezoid is at least 4.5 feet. What is the length of the f the trapezoid

Answer 1

`h=4.5\text{ feet}`

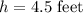
Explanation:

We have been given that a plot of land has an area 33.75 square feet. Jackson wants to put a 4-foot by 4 foot shed on the land. Jackson wants to put a 4-foot by 4 foot shed on the land. He can only do this if the height of the trapezoid is at least 4.5 feet.

We will use area of trapezoid to find the height of trapezoid.

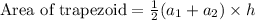`\text{Area of trapezoid}=(1)/(2)(a_1+a_2)* h`, where,

`a_1\text{ and }a_2=\text{ Parallel sides or bases of trapezoid}`,

`h=\text{Height}`.

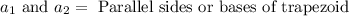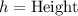We can see that parallel sides are 5 feet and 10 feet. We have been given that area of trapezoid is 33.75 square feet.

`33.75\text{ feet}^2=(1)/(2)(\text{ 5 feet + 10 feet})* h`

`33.75\text{ feet}^2=(1)/(2)(\text{ 15 feet})* h`

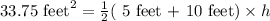
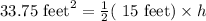
Switch sides:

`2*(1)/(2)(\text{ 15 feet})* h=2* 33.75\text{ feet}^2`

`\text{ 15 feet}* h=67.50\text{ feet}^2`

`\frac{\text{ 15 feet}* h}{\text{ 15 feet}}=\frac{67.50\text{ feet}^2}{\text{ 15 feet}}`

`h=4.5\text{ feet}`

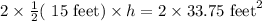
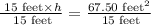
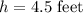
Since the height of trapezoid is 4.5 feet, therefore, Jackson can put a 4 foot by 4 foot shed on the land.

Answer 2

The height of the trapezoid is
`4.5\ ft`

Explanation:

we know that

The area of a trapezoid is equal to

`A=(1)/(2)(b1+b2)h`

In this problem we have

`A=33.75\ ft^(2)`

`b1=5\ ft`

`b2=10\ ft`

substitute in the formula and solve for h

`33.75=(1)/(2)(5+10)h`

`67.5=15h`

`h=67.5/15=4.5\ ft`