Answer:
C(x)=
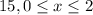
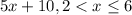
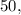 6<x≤∞
6<x≤∞
Explanation:
C(x) represents the monthly cost in dollars in terms of x, the number of gigabytes used in a month
Lets find C(x) on each interval (for every line graph)
first interval 0 to 2
the value of y is 15 on the interval 0 to 2
Its horizontal line . So equation is c(x)=the constant y value
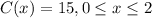
Second interval 2 to 6
Pick two points to get the equation of that line
(3,25) and (6,40)
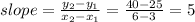
Equation of the line is using m=5 and (3,25)

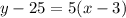

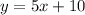

Now we look at the third interval
6 to infinity
For the third graph , the value of y is 50 (constant)
It is a horizontal line
So
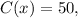 6<x≤∞
6<x≤∞
We got three equations for C(x)
C(x) is a piecewise function
C(x)=
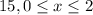
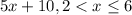
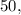 6<x≤∞
6<x≤∞