Question

7. Show all work to identify the discontinuity and zero of the function f of x equals 5 x over quantity x squared minus 25.

8. The aquarium has 6 fewer yellow fish than green fish. 40 percent of the fish are yellow. How many green fish are in the aquarium? Show your work.

Answer 1

Question 1:

For this case we have that the function
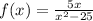`f (x) = \frac {5x} {x ^ 2-25}` is undefined or discontinuous where the denominator equals 0.

`x ^ 2-25 = 0\\x ^ 2 = 25\\x = \pm \sqrt {25}\\x_ {1} = + 5\\x_ {2} = - 5`

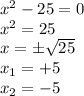
Thus, the function is undefined or discontinuous at +5 and -5.

To find the zeros of the function we match the function to zero and clear "x":

`\frac {5x} {x ^ 2-25} = 0`

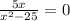
Factoring the denominator, taking into account that the roots are -5 and +5:

`\frac {5x} {(x + 5) (x-5)} = 0`

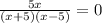
We multiply by
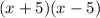`(x + 5) (x-5)`on both sides of the equation:

`5x = 0\\x = 0`

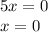
ANswer:

Discontinuity: + 5, -5

Zero: x = 0

Question 2:

For this case we propose a system of equations:

x: Be the variable that represents the yellow fish

y: Be the variable that represents the green fish

`x = y-6\\x = 0.4 (x + y)`

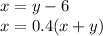
We manipulate the second equation:

`x = 0.4x + 0.4y\\x-0.4x = 0.4y\\0.6x = 0.4y\\y = \frac {0.6} {0.4} x\\y = 1.5x`

We substitute in the first equation:

`x = y-6\\x = 1.5x-6\\x-1.5x = -6\\-0.5x = -6\\x = \frac {-6} {- 0.5}\\x = 12`

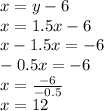
So, we have 12 yellow fish in the aquarium.

`y = 1.5 * 12\\y = 18`

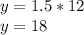
So, we have 18 green fish.

Answer:

12 yellow fish

18 green fish