Answer:
Opens up
Explanation:
Generally parabolas open up/down when you have an equation like this:
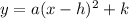
and when parabolas open to the left/right you have an equation as such:
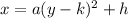
Btw the k and h being in different places is not a typo.
Anyways the reason for why
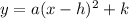 opens up, is for each x-value, you're only going to have one y-value. This is a parabola, so it's not a one-to-one function (where each output is unique), but it's still a function regardless.
opens up, is for each x-value, you're only going to have one y-value. This is a parabola, so it's not a one-to-one function (where each output is unique), but it's still a function regardless.
But when you have this equation:
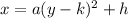 , there are two possible y-values, that will output the same x-value. Or in other words, each x-value (except the vertex) will have two outputs. So it's going to open sideways.
, there are two possible y-values, that will output the same x-value. Or in other words, each x-value (except the vertex) will have two outputs. So it's going to open sideways.
Anyways in the equation you provided we have the form:
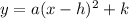 so the parabola is opening up or down. Now the only thing that really determines this is the "a" term"
so the parabola is opening up or down. Now the only thing that really determines this is the "a" term"
when a > 0 the parabola opens up
when a < 0 the parabola opens down
Note: This only applies when the parabola opens up/down
Since we have a positive "a" term, the parabola opens up. This makes sense, since the base of the exponent:
 is going to be growing faster than the constant:
is going to be growing faster than the constant:
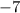 , so as
, so as
 the function will be increasing. It is of course decreasing as
the function will be increasing. It is of course decreasing as
 , since at the vertex that's the minimum. The reason for this is because:
, since at the vertex that's the minimum. The reason for this is because:
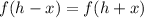 due to the symmetry of a parabola. So in our specific case:
due to the symmetry of a parabola. So in our specific case:
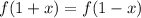 , this means that despite f(-100) having a lower x-value than f(50), it actually has a greater y-value, and has the same y-value as: f(102), since f(1-101) = f(1+101); meaning f(-100) = f(102). So as x goes towards zero, it's actually decreasing in this case. But after it passes the vertex, it will increase and go towards positive infinity.
, this means that despite f(-100) having a lower x-value than f(50), it actually has a greater y-value, and has the same y-value as: f(102), since f(1-101) = f(1+101); meaning f(-100) = f(102). So as x goes towards zero, it's actually decreasing in this case. But after it passes the vertex, it will increase and go towards positive infinity.