Answer: (a) 0.37
Explanation:
Given: The speed of cars on a stretch of road is normally distributed with an average 48 miles per hour with a standard deviation of 5.9 miles per hour.
i.e. Mean :
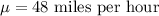
Standard deviation :

The formula to calculate z is given by :-

For the probability that a randomly selected car is violating the speed limit of 50 miles per hour (X≥ 50).
For x= 80
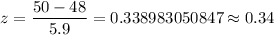
The P Value =
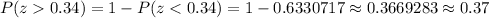
Hence, the probability that a randomly selected car is violating the speed limit of 50 miles per hour =0.37