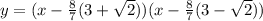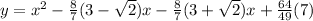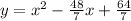Question

The roots of the equation x^2-6x+7=0 are a and b.

find a quadratic equation with roots a+1/b and b + 1/a.

please reply ASAP as i have an exam tomorrow!!​

Answer 1

`y=x^(2) -(48)/(7)x+(64)/(7)`

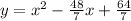
Explanation:

step 1

Find the roots of the quadratic equation

we know that

The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`x^(2) -6x+7=0`

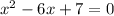
so

`a=1\\b=-6\\c=7`

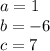
substitute in the formula

`x=\frac{6(+/-)\sqrt{-6^(2)-4(1)(7)}} {2(1)}`

`x=\frac{6(+/-)2√(2)} {2}`

`x=3(+/-)√(2)`

`x1=3(+)√(2)`

`x2=3(-)√(2)`

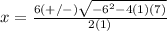
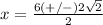
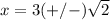
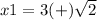
The roots of the equation are a and b

so

`a=3(+)√(2)`

`b=3(-)√(2)`

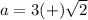
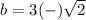
step 2

Find a quadratic equation with roots a+1/b and b + 1/a

so

`a+(1)/(b) =(3+√(2))+(1)/(3-√(2)) =(9-2+1)/(3-√(2)) =(8)/(3-√(2))=(8)/(3-√(2))*((3+√(2))/(3+√(2)))=(8)/(7)(3+√(2))`

`b+(1)/(a) =(3-√(2))+(1)/(3+√(2)) =(9-2+1)/(3+√(2)) =(8)/(3+√(2))=(8)/(3+√(2))*((3-√(2))/(3-√(2)))=(8)/(7)(3-√(2))`

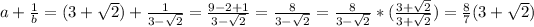
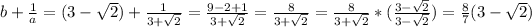
The quadratic equation is equal to

`y=(x-(8)/(7)(3+√(2)))(x-(8)/(7)(3-√(2)))`

`y=x^(2) -(8)/(7)(3-√(2))x-(8)/(7)(3+√(2))x+(64)/(49)(7)`

`y=x^(2) -(48)/(7)x+(64)/(7)`