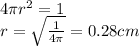Question

The radius of a sphere is increasing at a rate of 9 cm/ sec. Find the radius of the sphere when the volume and the radius of the sphere are increasing at the same numerical rate.

Answer 1

0.28 cm

Step-by-step explanation:

The volume of a sphere is given by:

`V=(4)/(3)\pi r^3`

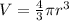
where r is the radius, which is dependent on the time, so r(t).

The rate of change of the volume is

`(dV)/(dt)=4 \pi r^2 (dr)/(dt)` (1)

where

`(dr)/(dt)` is the rate of change of the radius. We know that

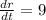`(dr)/(dt)=9` (cm/s)

And we want to find the value of the radius r when the rate of change of the volume is the same:

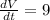`(dV)/(dt)=9` (cm^3/s)

So we can rewrite (1) as:

`9=4\pi r^2 \cdot 9`

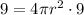
By solving it, we find

`4\pi r^2 = 1\\r = \sqrt{(1)/(4\pi)}=0.28 cm`