a. The wheel accelerates uniformly, so its constant acceleration is equal to the average acceleration:
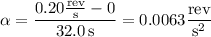
b. Yes. Since
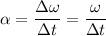
then multiplying
 by 2 means we double the change in angular speed, but the wheel starts from rest so only the final angular speed
by 2 means we double the change in angular speed, but the wheel starts from rest so only the final angular speed
 gets doubled.
gets doubled.