Answer:
2.5 m/s
Step-by-step explanation:
The total momentum before and after the collision must be conserved.
Before the collision, the total momentum is just given by Junior's momentum, since Ben is at rest. So,

where
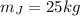 is Junior's mass
is Junior's mass
 is the Junior's initial velocity
is the Junior's initial velocity
So we find
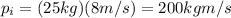
The final momentum will be equal to the initial momentum:

and it can be written as

where
 is Ben's mass
is Ben's mass
v is their final velocity
Solving for v,
