Question

The Chesapeake Bay tides vary between 4 feet and 6 feet. The tide is at its lowest point when time (t) is 0 and completes a full cycle in 12 hours. What is the amplitude, period, and midline of a function that would model this periodic phenomenon? Amplitude = 1 foot; period = 12 hours; midline: y = 5 Amplitude = 2 feet; period = 6 hours; midline: y = 1 Amplitude = 2 feet; period = 12 hours; midline: y = 5

Answer 1

A. Amplitude = 1 foot; period = 12 hours; midline: y = 5

Answer 2

The correct option is 1.

Explanation:

The general cosine function is

`y=A\cos (Bx+C)+D`

where, A is amplitude,
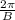`(2\pi)/(B)` is period, C is phase shift and D is midline.

It is given that the Chesapeake Bay tides vary between 4 feet and 6 feet. it means the minimum value is 4 and maximum value is 6.

Amplitude of the function is

`Amplitude=(Maximum-Minimum)/(2)`

`Amplitude=(6-4)/(2)`

`Amplitude=1`

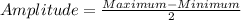
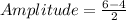
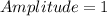
Therefore the amplitude of the function is y=5.

Midline of the function is

`Mid line=(Maximum+Minimum)/(2)`

`Mid line=(6+4)/(2)=5`

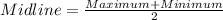
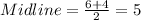
Therefore the midline of the function is y=5.

It completes a full cycle in 12 hours.

`Period=12` hours

`(2\pi)/(B)=12`

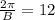
Period of the function is 12 hours. Therefore the correct option is 1.