Question

Solve the equation for x. If a solution is extraneous, be sure to identify it in your final answer.

Square root of x-2+8=x

Answer 1

Extraneous solution: x=6

Real solution: x=11

Step-by-step explanation

The given expression is

`√(x - 2) + 8 = x`

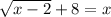
Add -8 to both sides:

`√(x - 2) + 8 + - 8= x + - 8`

`\implies√(x - 2) = x - 8`

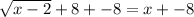
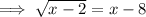
Square both sides.

`\implies(√(x - 2) )^(2) =( x - 8)^(2)`

`x - 2=( x - 8)^(2)`

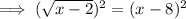
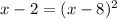
We expand the to get

`x - 2 = {x}^(2) - 16x + 64`

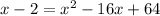
Write in standard quadratic form.

`{x}^(2) - 16x - x + 64 + 2 = 0`

`{x}^(2) - 17x + 66 = 0`

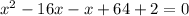
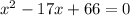
Factor to get:

`(x - 6)(x - 11) = 0`

`x = 6 \: or \: \: x = 11`

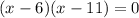
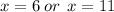
We check for extraneous solutions by substituting each value of x into the original equation.

When x=6

`√(6 - 2) + 8 = 6`

`√(4) + 8 =6`

`2 + 8 = 10 \\e8`

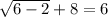
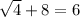
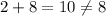
Hence x=6 is an extraneous solution.

When x=11

`√(11- 2) + 8 = 11`

`√(9) + 8 = 11`

`3 + 8 = 11`

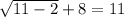
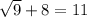
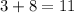
This statement is true.

Hence x=11 is the only solution.