Question

If a circle has a diameter with end points: (4 + 6i) and (-2 + 6i),

1. Show me how you would determine the length of the diameter and radius.
2. Show me how you would determine the center of the circle.
3. Determine, mathematically, if (1+9i) lies on the circle. Show how you proved it mathematically.
4. Determine, mathematically, if (2-i) lies on the circle. Show how you proved it mathematically.

Answer 1

To determine the length of the diameter and radius, use the distance formula. The center of the circle can be found by finding the midpoint of the diameter's end points. To determine if a point lies on the circle, use the distance formula to compare the distance between the point and the center to the radius.

Step-by-step explanation:

1. Determining the length of the diameter and radius:

To find the length of the diameter, we can use the distance formula. The distance between two complex numbers (a + bi) and (c + di) is given by the formula √((c-a)^2 + (d-b)^2). In this case, the two end points of the diameter are (4 + 6i) and (-2 + 6i). Using the formula, the distance is √((-2-4)^2 + (6-6)^2) = √((-6)^2 + 0) = √(36) = 6.

The radius of a circle is half the length of the diameter. Therefore, the radius of this circle is 6/2 = 3.

2. Determining the center of the circle:

The center of the circle is the midpoint between the two end points of the diameter. To find the midpoint, we can take the average of the x-coordinates and the average of the y-coordinates. In this case, the x-coordinates of the end points are 4 and -2, and the y-coordinates are 6. Taking the averages, the x-coordinate of the center is (4 + (-2))/2 = 1 and the y-coordinate of the center is (6 + 6)/2 = 6. Therefore, the center of the circle is the complex number 1 + 6i.

3. Determining if (1 + 9i) lies on the circle:

To determine if a point lies on the circle, we can check if the distance between the center of the circle and the point is equal to the radius. Using the distance formula again, the distance between the center (1 + 6i) and the point (1 + 9i) is √((1-1)^2 + (9-6)^2) = √(0 + 9) = √(9) = 3. Since the distance is equal to the radius, we can conclude that (1 + 9i) does lie on the circle.

4. Determining if (2 - i) lies on the circle:

Using the same process, we find that the distance between the center (1 + 6i) and the point (2 - i) is √((2-1)^2 + (-1-6)^2) = √(1 + 49) = √(50). Since √(50) is not equal to the radius (3), we can conclude that (2 - i) does not lie on the circle.

Answer 2

Part 1) The diameter is
`D=6\ units` and the radius is equal to
`r=3\ units`

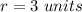
Part 2) The center of the circle is (1+6i)

Part 3) The point (1+9i) lies on the circle

Part 4) The point (2-i) does not lies on the circle

Step-by-step explanation:

Part 1) Show me how you would determine the length of the diameter and radius.

we have that

The circle has a diameter with end points: (4 + 6i) and (-2 + 6i)

we know that

The distance between the end points is equal to the diameter

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

(4 + 6i) ----> (4,6)

(-2 + 6i) ---> (-2,6)

substitute the values

`d=\sqrt{(6-6)^(2)+(-2-4)^(2)}`

`d=\sqrt{(0)^(2)+(-6)^(2)}`

`d=6\ units`

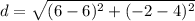
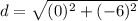
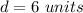
therefore

The diameter is
`D=6\ units`

The radius is equal to
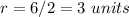`r=6/2=3\ units` ---> the radius is half the diameter

Part 2) Show me how you would determine the center of the circle

we know that

The center of the circle is equal to the midpoint between the endpoints of the diameter

The circle has a diameter with end points: (4 + 6i) and (-2 + 6i)

The formula to calculate the midpoint between two points is equal to

`M((x1+x2)/(2),(y1+y2)/(2))`

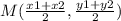
substitute

`M((4-2)/(2),(6+6)/(2))`

`M(1,6})`

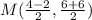
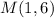
therefore

(1,6) ----> (1+6i)

The center of the circle is (1+6i)

Part 3) Determine, mathematically, if (1+9i) lies on the circle. Show how you proved it mathematically

Find the equation of the circle

`(x-h)^(2)+(y-k)^(2)=r^(2)`

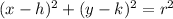
we have

The center is (1+6i) -----> (1,6)

r=3 units

substitute

`(x-1)^(2)+(y-6)^(2)=3^(2)`

`(x-1)^(2)+(y-6)^(2)=9`

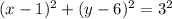
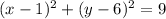
Verify if the point (1+9i) lies on the circle

Remember that

If a point lies on the circle, then the point must satisfy the equation of the circle

Substitute the value of x and the value of y in the equation and then compare the results

we have

the point (1+9i) -----> (1,9)

`(1-1)^(2)+(9-6)^(2)=9`

`(0)^(2)+(3)^(2)=9`

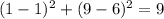
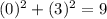
`9=9` -----> is true

therefore

The point (1+9i) lies on the circle

Part 4) Determine, mathematically, if (2-i) lies on the circle. Show how you proved it mathematically

The equation of the circle is equal to

`(x-1)^(2)+(y-6)^(2)=9`

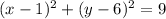
Verify if the point (2-i) lies on the circle

Remember that

If a point lies on the circle, then the point must satisfy the equation of the circle

Substitute the value of x and the value of y in the equation and then compare the results

we have

the point (2-i) -----> (2,-1)

`(2-1)^(2)+(-1-6)^(2)=9`

`(1)^(2)+(-7)^(2)=9`

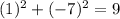
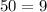`50=9` -----> is not true

therefore

The point (2-i) does not lies on the circle