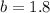Answer:
Slope
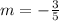
point-slope form

slope-intersection form

Explanation:
The equation of a line in the point-slope form has the following formula:

Where m is the slope and
 is a point belonging to the line.
is a point belonging to the line.
The equation of a line in the slope-intersection form has the following formula:

Where b is the intersection of the line with the y axis.
To calculate the slope of the line knowing 2 points we use the following formula:
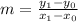
In this case:

So
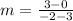
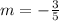
So the equation of a line in the point-slope form
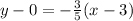

The equation of a line in the slope-intersection form is:


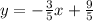

with