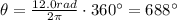Answer:
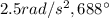
Step-by-step explanation:
The angular acceleration is given by:
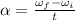
where
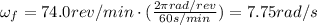 is the final angular speed
is the final angular speed
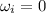 is the initial angular speed
is the initial angular speed
t = 3.10 s is the time interval
Solving the equation,
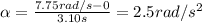
Now we can find the angular displacement by using:
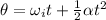
Substituting,
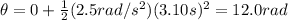
In degrees: