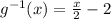For this case we must find the inverse of the following function:
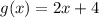
Replace g(x) with y:
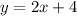
We exchange the variables:
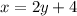
We solve for "y":
We subtract 4 on both sides of the equation:
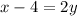
We divide between 2 on both sides of the equation:

We change y by
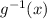 :
:
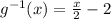
Answer: