(a)/(x-8) +(b)/(x+4) =(2x-64)/((x-8)(x+4)) solve for a and b

Question

`(a)/(x-8) +(b)/(x+4) =(2x-64)/((x-8)(x+4))`
solve for a and b

Answer 1

a=-4 and b=6

Explanation:

`(a)/(x-8) +(b)/(x+4) =(2x-64)/((x-8)(x+4))`

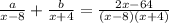
First, add the fractions by finding the common denominator.

In this case, (x-8)(x+4).

`(a(x+4) + b(x-8))/((x-8)(x+4)) =(2x-64)/((x-8)(x+4))`

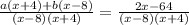
Therefore, the numerators are equal:

`a(x+4) + b(x-8) =2x-64`

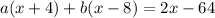
Simplify:

`ax+4a + bx-8b =2x-64\\(a+b)x+4a-8b=2x-64`

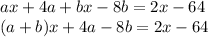
Now match the coefficients.

`a+b=2, 4a-8b=-64`

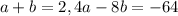
Solve the system of equations. I'll use substitution, but you can also use elimination if you prefer.

`4a-8b=-64\\a-2b=-16\\(2-b)-2b=-16\\2-3b=-16\\-3b=-18\\b=6\\a=-4`

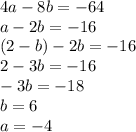
Therefore, a=-4 and b=6.

Answer 2

a = -4

b = 6

Explanation:

See attached