Answer: First Option
Walter needs to make at least 5 more cookies but no more than 40
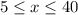
Explanation:
If we call x the number of cookies that Walter needs to make, then we know that the amount of cookies will be:
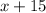
Then this amount must be greater than or equal to 20 and must be less than or equal to 55 then.
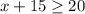 and
and
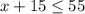
This is:
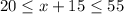
We solve the inequality for x.

Then the amount of cookies that Walter must make must be greater than or equal to 5 and less than or equal to 40