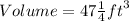Question

A rectangular prism has a length of 2 1/4 feet, a width of 6 feet, and a height of 3 1/2 feet.

What is the volume of the prism?



Enter your answer in the box.


ft³

Answer 1

For this case we have by definition, that the area of a rectangular prism is given by:

`V = A_ {b} * h`

Where:

`A_ {b}:` is the area of the base

h: It's the height

Before finding
`A_ {b}`we convert the mixed numbers to fractions:

length:
`2 \frac {1} {4} = \frac {4 * 2 + 1} {4} = \frac {9} {4}`

width: 6

Height:
`3 \frac {1} {2} = \frac {2 * 3 + 1} {2} = \frac {7} {2}`

So, we have to:
`A_ {b} = \frac {9} {4} * 6 = \frac {54} {4} = 13.5`

Finally, the volume is given by:

`V = 13.5 * \frac {7} {2} =47.25\ ft ^ 3`

Answer:

`47.25 \ ft ^ 3`

Answer 2

`Volume = 47(1)/(4) {ft}^(3)`

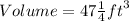
Step-by-step explanation

The formula for calculating the volume of a rectangular prism is

`Volume = l * b * h`

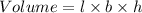
Where

`l = 2 (1)/(4) ft`

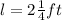
is the length of the rectangular box,

`w = 6ft`

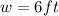
is the width and

`h = 3 (1)/(2) ft`

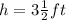
is the height of the rectangular prism.

We plug in the given dimensions into the formula to get:

`Volume = 2 (1)/(4) * 6 * 3 (1)/(2)`

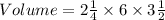
Convert the mixed numbers to improper fraction to get:

`Volume = (9)/(4) * 6 * (7)/(2)`

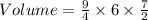
Multiply out to get

`Volume = (189)/(4) {ft}^(3)`

Or

`Volume = 47(1)/(4) {ft}^(3)`