Answer:
Table C
Explanation:
we have
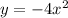
The quadratic equation in standard form is equal to
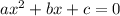
so
In this problem
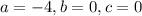
The y-intercept is the value of y when the value of x is equal to zero
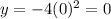
The y-intercept is the point (0,0)
The coefficient a is negative, therefore the parabola open down