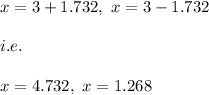Question

Given x^4 − 4x^3 = 6x^2 − 12x, what are the approximate values of the non-integral roots of the polynomial equation?

Answer 1

The approximate values of the non-integral roots of the polynomial equation are:

1.27 and 4.73

Explanation:

We are given an algebraic equation as:

`x^4-4x^3=6x^2-12x`

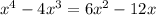
i.e. it could be written as:

`x^4-4x^3-6x^2+12x=0\\\\i.e.\\\\x(x^3-4x^2-6x+12)=0`

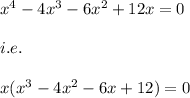
Since, we pulled out the like term i.e. "x" from each term.

Now we know that
`x=-2` is a root of the term:

`x^3-4x^2-6x+12`

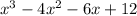
Hence, we split the term into factors as:

`x^3-4x^2-6x+12=(x-2)(x^2-6x+6)`

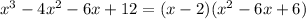
Now, finally the equation could be given by:

`x(x-2)(x^2-6x+6)=0`

Hence, we see that:

`x=0,\ x-2=0\ and\ x^2-6x+6=0\\\\i.e.\\\\x=0,\ x=2\ and\ x^2-6x+6=0`

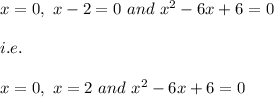
`x=0\ and\ x=2` are integers roots.

Now, we find the roots with the help of quadratic equation:

`x^2-6x+6=0`

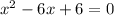
( We know that the solution of the quadratic equation:

`ax^2+bx+c=0` is given by:

`x=(-b\pm √(b^2-4ac))/(2a)` )

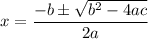Here we have:

`a=1,\ b=-6\ and\ c=6`

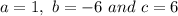
Hence, the solution is:

`x=(-(-6)\pm √((-b)^2-4* 1* 6))/(2* 1)\\\\i.e.\\\\x=(6\pm √(36-24))/(2)\\\\i.e.\\\\x=(6\pm √(12))/(2)\\\\i.e.\\\\x=(6)/(2)\pm (2√(3))/(2)\\\\i.e.\\\\x=3\pm 3\\\\i.e.\\\\x=3+√(3),\ x=3-√(3)`

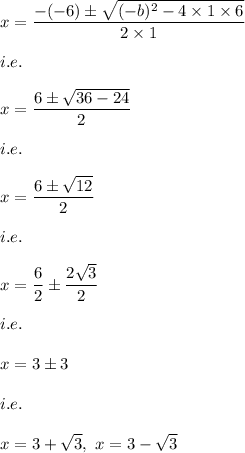
Now, we put
`√(3)=1.732`

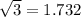
Hence, the approximate value of x is:

`x=3+1.732,\ x=3-1.732\\\\i.e.\\\\x=4.732,\ x=1.268`

Answer 2

the values of the non-integral roots of the polynomial equation are:

4.73 and 1.27.

Explanation:

To find the roots of the polynomial equation, we need to factorize the equation:

x^4 − 4x^3 = 6x^2 − 12x ⇒ x^4 − 4x^3 -6x^2 +12x = 0

⇒ x(x+2)(x -3 + sqrt(3))(x -3 - sqrt(3))

Then, the non integral roots are:

x1 = 3 - sqrt(3) = 1.26 ≈ 1.27

x2 = 3 + sqrt(3) = 4.73

Then, the values of the non-integral roots of the polynomial equation are:

4.73 and 1.27