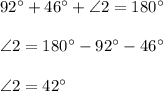Answer:
Second option.
Explanation:
The angle
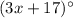 and the angle
and the angle
 are alternate exterior angles, then they are congruent. So we can can find "x":
are alternate exterior angles, then they are congruent. So we can can find "x":
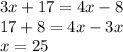
Then, the angle
 is:
is:
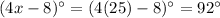
You can observe that the angle identified in the figure attached as "3" and the angle 46° are Alternate interior angles, then they are congruent.
Since the sum of the measures of the angles that measure 92°, 46° and the angle "2" is 180°, we can find the measure of the angle "2" by solving this expression: