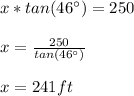Question

An engineer on the ground is looking at the top of a building. The angle of elevation to the top of the building is 46°. The engineer knows the building is 250 ft tall. What is the distance from the engineer to the base of the building to the nearest whole foot?

Answer 1

Answer: 241 feet.

Explanation:

Observe the figure attached, where "x" is the distance from the engineer to the base of the building to the nearest whole foot.

We need to remember this identity:

`tan\alpha=(opposite)/(adjacent)`

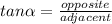
In this case we know that:

`\alpha=46\°\\opposite=250\\adjace nt=x`

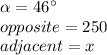
Therefore, the next step is to substitute these values into
`tan\alpha=(opposite)/(adjacent)`:

`tan(46\°)=(250)/(x)`

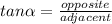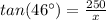
And the final step is to solve for "x":

`x*tan(46\°)=250\\\\x=(250)/(tan(46\°))\\\\x=241ft`

Answer 2

=241 ft

Explanation:

The building is opposite the angle of elevation. Thus using trigonometric ratios it is easier to use Tangent of the elevation angle to find the distance to the foot of the building (adjacent).

Tan ∅ = opposite/ adjacent

Tan ∅= height of the building/ distance between the engineer and the building

distance= height/tan ∅

=250/tan 46°

=241 ft

=