Question

At a certain temperature the rate of this reaction is first order in HI with a rate constant of :0.0632s2HIg=H2g+I2g Suppose a vessel contains HI at a concentration of 1.28M . Calculate how long it takes for the concentration of HI to decrease to 17.0% of its initial value. You may assume no other reaction is important. Round your answer to 2 significant digits.

Answer 1

`\boxed{\text{28.0 s}}`

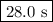
Step-by-step explanation:

Whenever a question asks you, "How long does it take to reach a certain concentration?" or something like that, you must use the appropriate integrated rate law expression.

The integrated rate law for a first-order reaction is

`\ln \left (([A]_(0))/([A]) \right ) = kt`

Data:

[A]₀ = 1.28 mol·L⁻¹

[A] = 0.17 [A]₀

k = 0.0632 s⁻¹

Calculation:

`\begin{array}{rcl}\ln \left (([A]_(0))/(0.170[A]_(0)) \right ) & = & 0.0632t\\\\\ln \left (5.882) & = & 0.0632t\\1.772 & = & 0.0632t\\\\t & = & (1.772)/(0.0632)\\\\t & = & \textbf{{28.0 s}}\\\end{array}\\\text{It will take } \boxed{\textbf{28.0 s}} \text{ for [HI] to decrease to 17.0 \% of its original value.}`