ANSWER
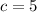
Step-by-step explanation
A quadratic equation is said to be in standard form when it is in the form
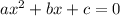
where a, b, c are real numbers.
The given quadratic equation is
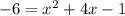
When we add 6 to both sides, we obtain,
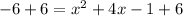

Or
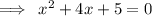
This is what Alexandra got after he wrote the quadratic equation in standard form.
By comparing this equation to
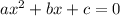
we have a=1, b=4 and c=5.