Answer:
C. 28
Explanation:
From the diagram diagram;
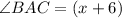 and
and
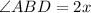 .
.
- The opposite sides of a rhombus are parallel.
- The diagonals act as transversals.
- Therefore the co-interior angles will add up to 180 degrees.
The pair of co-interior angles are
 and
and
 .
.
Also the diagonals of a rhombus bisect corner angles.
This implies that:
 .
.
 .
.
The co-interior angles are supplementary so we form the equation:
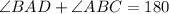

Expand the parenthesis to get:
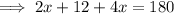
Group the similar terms:
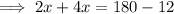
Simplify

Divide both sides by 6.
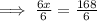
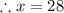
The correct answer is C.