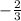ANSWER
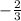
EXPLANATION
The given given equation is
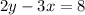
We need to rewrite this equation in the slope-intercept form:
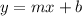
We add 3x to both sides.
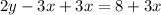
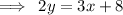
We divide through by 2 to get,
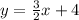
The slope of this line is
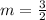
Let the slope of the line perpendicular to this line be 'n' .
Then the product of the slopes of two perpendicular lines is always negative 1.
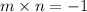
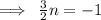
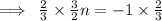
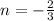
Therefore the slope of the new line is