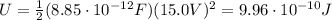Question

A dielectric-filled parallel-plate capacitor has plate area A = 30.0 cm2 , plate separation d = 9.00 mm and dielectric constant k = 3.00. The capacitor is connected to a battery that creates a constant voltage V = 15.0 V . Throughout the problem, use ϵ0 = 8.85x10-12 C2/N.m2 . Find the energy U1 of the dielectric-filled capacitor.

Answer 1

`9.96\cdot 10^(-10)J`

Step-by-step explanation:

The capacitance of the parallel-plate capacitor is given by

`C=\epsilon_0 k (A)/(d)`

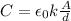
where

ϵ0 = 8.85x10-12 C2/N.m2 is the vacuum permittivity

k = 3.00 is the dielectric constant

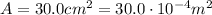`A=30.0 cm^2 = 30.0\cdot 10^(-4)m^2` is the area of the plates

d = 9.00 mm = 0.009 m is the separation between the plates

Substituting,

`C=(8.85\cdot 10^(-12)F/m)(3.00 ) (30.0\cdot 10^(-4) m^2)/(0.009 m)=8.85\cdot 10^(-12) F`

Now we can calculate the energy of the capacitor, given by:

`U=(1)/(2)CV^2`

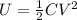
where

C is the capacitance

V = 15.0 V is the potential difference

Substituting,

`U=(1)/(2)(8.85\cdot 10^(-12)F)(15.0 V)^2=9.96\cdot 10^(-10)J`