Question

The zeros of a parabola are 6 and −5. If (-1, 3) is a point on the graph, which equation can be solved to find the value of a in the equation of the parabola?

3 = a(−1 + 6)(−1 − 5)
3 = a(−1 − 6)(−1 + 5)
−1 = a(3 + 6)(3 − 5)
−1 = a(3 − 6)(3 + 5)

Answer 1

3 = a(−1 − 6)(−1 + 5)

Explanation:

I took the test on edge

Answer 2

`3= a( - 1 +6)( - 1 - 5)`

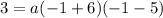
EXPLANATION

The equation of a parabola in factored form is

`y = a(x + m)(x + n)`

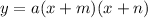
where 'a' is the leading coefficient and 'm' and 'n' are the zeros.

From the question, the zeros of the parabola are 6 and −5.

This implies that,

`m = 6 \: \: and \: \: n = - 5`

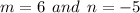
We plug in these zeros to get:

`y= a(x +6)(x - 5)`

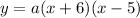
If (-1, 3) is a point on the graph of this parabola,then it must satisfy its equation.

We substitute x=-1 and y=3 to obtain:

`3= a( - 1 +6)( - 1 - 5)`

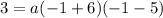
The first choice is correct.