Answer:
There are no solutions to the inequality.
Explanation:
|x - 3| < x – 3
1. Separate the inequality into two separate ones.
(1) x – 3 < x – 3
(2) x – 3 < -(x – 3)
2. Solve each equation separately
(a) Equation (1)
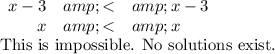
(b) Equation (2)
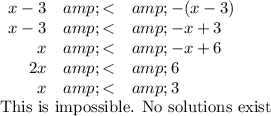
For example, if x = 0, we get
|0 - 3| < 0 - 3 or
3 < -3