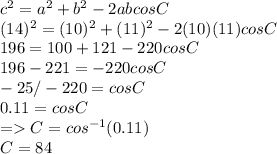Answer:
Law of Cosines
Angle A = 45°
Angle B = 51°
Angle C = 84°
Explanation:
Law of sines is used when we are given
a) two angles and one side or
b) two sides and non-included angle
Law of cosines is used when we are given
a) three sides or
b) two sides and included angle
In the given question we are given three sides so, Law of Cosines will be used to solve the triangle.
Law of Cosines is:
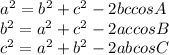
We will find the three angles A ,B and C of the triangle using above formula.
a= 10, b=11, c=14
Putting values and finding angle A
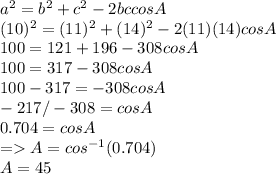
Now finding angle B
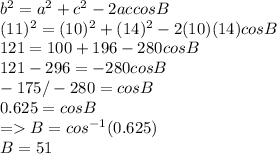
Now finding angle C