Answer:
b.

Explanation:
We have to find the linear which has same slope as the slope represented by the table.
Slope formula :m=
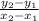
By using the formula and substitute
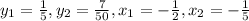
Slope=
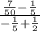
Slope=
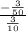
Slope=
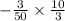
Slope=
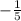
a.
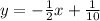
Compare with

we get m=
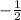
Slope=
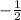
Hence, option A is false.
b.

Slope of given function=
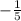
It is true.
c.
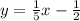
Slope of given function=
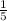
Hence, option is false.
d.
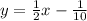
Slope of given function=

Hence, option is false.