Answer:
The coordinates of the point in question is (1, 3).
Explanation:
Point (-1, 7) is above and to the left of the point (4, -3). The point in question is to the right and below the point (-1, 7).
What will be the horizontal distance between the point (-1, 7) and the point in question?
The horizontal distance between the point (-1, 7) and (4, -3) is 5. Let the horizontal distance between the point (-1, 7) and the point in question be
 . Let the horizontal distance between the point in question and point (4, -3) be
. Let the horizontal distance between the point in question and point (4, -3) be
 .
.
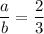 .
.
 .
.
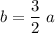 .
.
However,
 .
.
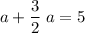 .
.
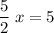 .
.
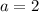 .
.
In other words, the point in question is 2 units to the right of the point (-1, 7). The x-coordinate of this point shall be
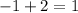 .
.
The vertical distance between the point (-1, 7) and the point (4, -3) is 10. Similarly, the point in question is
 units below the point (-1, 7). The y-coordinate of this point will be
units below the point (-1, 7). The y-coordinate of this point will be
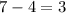 .
.
Thus, the point in question is (1, 3).