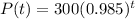Question

Drag the tiles to the boxes to form correct pairs. Not all tiles will be used

Match each situation to its corresponding expression.

Answer 1

Reading from top to bottom. Answers are as follows:

1. 7(2)^t

2. 3000(0.93)^t

3. 300(1.015)^t

4. 300(0.985)^t

Answer 2

Answer with explanation:

We know that the exponential function is given by:

`f(x)=ab^x`

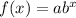
where a is the initial amount.

and b is the change in the amount and is given by:

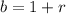`b=1+r` if the function is increasing by a rate of r

and
`b=1-r` if the function is decreasing by a rate of r.

a)

The initial amount of fish in the trout are: 7

i.e. a=7

Also, the population doubles every year.

This means that that b=2

Hence, the population after t years is given by the function P(t) as:

`P(t)=7(2)^t`

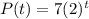
b)

The original amount of the machine is: $ 3,000

i.e. a=3,000

Also, the value of machine decreases by a rate of 7%

i.e.

`r=7\%\\\\i.e.\\\\r=0.07`

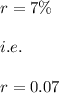
Hence, we have:

`b=1-r\\\\i.e\\\\b=1-0.07\\\\i.e.\\\\b=0.93`

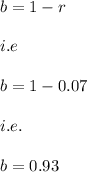
Hence, the function which represent the price of the machine after t years i.e. P(t) is given by:

`P(t)=3000(0.93)^t`

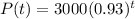
c)

The initial population of colony of ants i.e. a=300.

The number of ants increases at a rate of 1.5% every month.

i.e.
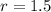
`r=1.5%\\\\i.e.\\\\r=0.015`

i.e.

`b=1+r\\\\i.e.\\\\b=1+0.015\\\\i.e.\\\\b=1.015`

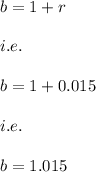
Hence, the function P(t) which represents the population of ants after t months is given by:

`P(t)=300(1.015)^t`

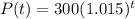
d)

The initial infected cells i.e. a=300

The infected cells are decaying at a rate of 1.5% per minute.

i.e.

`r=1.5%\\\\i.e.\\\\r=0.015`

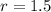
Since, there is a decay hence,

`b=1-r\\\\i.e.\\\\b=1-0.015\\\\i.e.\\\\b=0.985`

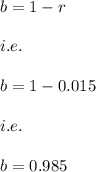
Hence, the function P(t) which represents the number of infected cells after t minutes is given by:

`P(t)=300(0.985)^t`