Question

Consider each table of values

of the three functions,
f & h
none
f & g
g & h
all three
represent linear relationships

Answer 1

g and h

Explanation:

both g and h have constant relationships while f's f(x) values aren't constant so it doesn't have a linear relationship

Answer 2

Of the three functions g and h represent linear relationship.

Explanation:

If a function has constant rate of change for all points, then the function is called a linear function.

If a lines passes through two points, then the slope of the line is

`m=(x_2-x_1)/(y_2-y_1)`

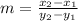
The slope of function f(x) on [1,2] is

`m_1=(11-5)/(2-1)=6`

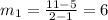
The slope of function f(x) on [2,3] is

`m_2=(29-11)/(3-2)=18\\eq m_1`

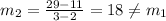
Since f(x) has different slopes on different intervals, therefore f(x) does not represents a linear relationship.

From the given table of g(x) it is clear that the value of g(x) is increased by 8 units for every 2 units. So, the function g(x) has constant rate of change, i.e.,

`m=(8)/(2)=4`

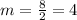
From the given table of h(x) it is clear that the value of h(x) is increased by 6.8 units for every 2 units. So, the function h(x) has constant rate of change, i.e.,

`m=(6.8)/(2)=3.4`

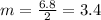
Since the function g and h have constant rate of change, therefore g and h represent linear relationship.