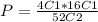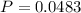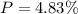Answer:
Explanation:
First we calculate the number of possible ways to select 2 cards an ace and a card of 10 points.
There are 4 ace in the deck
There are 16 cards of 10 points in the deck
To make this calculation we use the formula of combinations

Where n is the total number of letters and r are chosen from them
The number of ways to choose 1 As is:
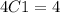
The number of ways to choose a 10-point letter is:
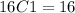
Therefore, the number of ways to choose an Ace and a 10-point card is:
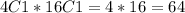
Now the number of ways to choose any 2 cards from a deck of 52 cards is:
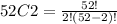
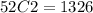
Therefore, the probability of obtaining an "blackjack" is: