Question

Consider the following geometric series. Rewrite the series using sigma notation. 4-10+25-62.5+156.25-390.625

Answer 1

See below.

Explanation:

The common ratio = -10/4 = -5/2 and the first term is 4.

The sigma notation is:

n=6

∑ 4(-5/2)^n-1. (answer).

n=1

Answer 2

`\sum_(n=1)^(n=6) 4((-5)/(2) )^(n-1)`

Explanation:

We are given the geometric series
`4 + -10+ 25+ -62.5+ 156.25+ -390.625`

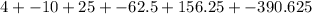
General geometric series is of the form

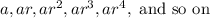`a, ar, ar^2, ar^3, ar^4,\text{ and so on}`, where a is the first term and r is the common ration.

The common ratio for given geometric series is
`\frac{\text{Second Term}}{\text{First Term}}` =
`(-10)/(4) = (-5)/(2)`

`a = 4\\r = (-5)/(2)`

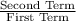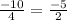
To write the series in summation form we use:

`\sum_(k=0)^(k=n) a(r)^(k)`

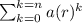
Thus, the given geometric series is

`\sum_(n=1)^(n=6) 4((-5)/(2) )^(n-1)`