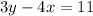You are on the right tracks.
Since angle ABC is a right angle, that means lines AB and BC are perpendicular.
Therefore the gradient of BC = the negative reciprocal of the gradient of AB. We can use this to form an equation to find what K is.
You have already worked out the gradient of AB ( 1/2) (note it's easier to leave it as a fraction)
Now lets get the gradient of BC:
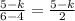
Remember: The gradient of BC = the negative reciprocal of the gradient of AB. So:
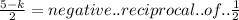
So:
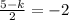 (Now just solve for k)
(Now just solve for k)
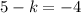
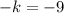 (now just multiply both sides by -1)
(now just multiply both sides by -1)
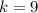
That means the coordinates of C are: (4, 9)
We can now use this to work out the gradient of line AC, and thus the equation:
Gradient of AC:
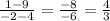
Now to get the equation of the line, we use the equation:
y - y₁ = m( x - x₁)
Let's use the coordinates for A (-2, 1), and substitute them for y₁ and x₁ and lets substitute the gradient in for m:
y - y₁ = m( x - x₁)
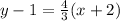 (note: x - - 2 = x + 2)
(note: x - - 2 = x + 2)
Now lets multiply both sides by 3, to get rid of the fraction:
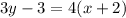 (now expand the brackets)
(now expand the brackets)
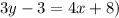
Finally, we just rearrange this to get the format: ay + bx = c
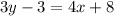

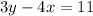
And done!:
________________________________
Answer:
The equation of a line that passes through point A and C is: