Question

Which set of ordered pairs has point symmetry with respect to the origin (0, 0)? (-12, 5), (-5, 12) (-12, 5), (12, -5) (-12, 5), (-12, -5) (-12, 5), (12, 5)

Answer 1

(-12, 5), (12, -5)

Explanation:

Since, the rule of point symmetry with respect to the origin is,

`(x,y)\rightarrow (-x, -y)`

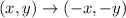
That is, the mirror image of the point (x, y) with respect to the origin is (-x,-y),

Thus, in the point symmetry with respect to the origin,

`(-12, 5)\rightarrow (-(-12), -5))`

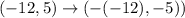
So, the mirror image of point (-12,5) with respect to the origin is (12, -5),

Hence, the set of ordered pairs has point symmetry with respect to the origin is,

(-12, 5), (12, -5)

Second option is correct.

Answer 2

(-12, 5), (12, -5)

Explanation:

Reflection across the origin is the transformation ...

(x, y) ⇒ (-x, -y)

Look for coordinates that are the opposites of their counterparts. You will find the appropriate answer choice is ...

(-12, 5), (12, -5)