Question

Arlo invested $4000 in an account that earns 5.5% interest, compounded annually. The formula for compound interest is A(t)=P(1+i)^t. How much did Arlo have in the account after 4 years?

Answer 1

`\bf ~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill &\$4000\\ r=rate\to 5.5\%\to (5.5)/(100)\dotfill &0.055\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{annually, thus once} \end{array}\dotfill &1\\ t=years\dotfill &4 \end{cases} \\\\\\ A=4000\left(1+(0.055)/(1)\right)^(1\cdot 4)\implies A=4000(1.055)^4\implies A\approx 4955.2986`

Answer 2

$ 4955.30 ( approx )

Explanation:

The formula for compound interest is,

`A(t)=P(1+i)^t`

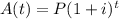
Where, P is the principal amount,

i is the rate per period,

t is the number of periods,

Here, P = $ 4000,

i = 5.5% = 0.055

t = 4 years,

By substituting the values,

The amount in the account after 4 years would be,

`A=4000(1+0.055)^4=4000(1.055)^4=4955.2986025\approx \$4955.30`