Question

The pulse rate (in bpm) of a random sample of 30 Peruvian Indians was collected. The mean pulse rate of the sample was 70.2 and the standard deviation was 10.51. Compute the 95% confidence interval for the population mean.

Answer 1

= 70.2 ± 3.761 bpm

Explanation:

The question is on calculating the confidence interval for a population mean

The general expression is

CI = x ± z * δ/√n where;

CI = confidence interval,

x = mean of sample,

δ = standard deviation,

n= is sample size

z = z* value from standard normal distribution according to confidence level given.

Given that;

n= 30 x =70.2 δ=10.51 z* for 95% CI = 1.96

Then applying the expression

CI = x ± z * δ/√n

`=√(n) = √(30) =5.477\\\\=(10.51)/(5.477) =1.919*1.96=3.761\\\\`

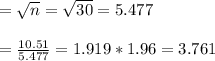
Cl = 70.2±3.761

= 70.2 ± 3.761 bpm