Question

How do you solve this?

Answer 1

The equation of a circle is:

(x - h)² + (y - k)² = radius²

Note:

h = x coordinate for the centre of the circle

k = y coordinate for the centre of the circle

The equation for the circle in the question is:

(x - 6)² + (y - 5)² = 16

So the coordinates for the centre of the circle is:

(6, 5)

------------------------

Since PQ is the diameter of the circle, that means the coordinates for the midpoint of PQ would also be the coordinates for the centre of the circle

That means:

( (x coords of P and Q) / 2 , (y coords of P and Q) / 2 )= (6 , 5)

So x-coords of Q:

`(10 + x)/(2) = 6`

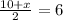
10 + x = 12

x = 2

y-coords of Q

`(-5+ x)/(2) = -5`

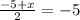
-5 + x = - 10

x = 5

So the coordinates for Q are:

(2, -5)

---------------------------------------------

Answer:

Option A) (2, - 5)

Answer 2

`\bf \textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \qquad center~~(\stackrel{}{ h},\stackrel{}{ k})\qquad \qquad radius=\stackrel{}{ r} \\\\[-0.35em] ~\dotfill\\\\ (x-6)^2+(y+5)^2=16\implies [x-\stackrel{h}{6}]^2+[y-(\stackrel{k}{-5})]^2=\stackrel{r}{4^2}~\hfill \begin{cases} \stackrel{center}{(6,-5)}\\ \stackrel{radius}{4} \end{cases}`

Check the picture below.