Question

The tension in the string of a simple pendulum is:

a. constant

b. Maximum in the extreme position

c. Zero in the mean position

d. None of the above

Answer 1

D. None of the above

Step-by-step explanation:

There are only two forces acting on a pendulum:

- The force of gravity (downward)

- The tension in the string

We can consider the axis along the direction of the string: here we have the tension T, acting towards the pivot, and the component of the weight along this direction, acting away from the pivot. Their resultant must be equal to the centripetal force, so we can write:

`T-mg cos \theta = m(v^2)/(r)\\T=m(v^2)/(r)+mg cos \theta`

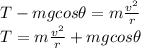
where

T is the tension in the string

`\theta` is the angle between the tension and the vertical

m is the mass

g is the acceleration of gravity

v is the speed of the pendulum

r is the length of the string

From the formula we see that the value of the tension, T, depends only on the value of v (the speed) and
`\theta`, the angle. We notice that:

- Since
`\theta` and v constantly change, T must change as well

- At
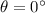`\theta=0^(\circ)` (equilibrium position),
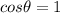`cos \theta=1` (maximum value), and also the speed v is maximum, so the tension has the maximum value at the equilibrium position

- For
`\theta` increasing, the
`cos \theta` decreases and the speed v decreases as well, so the tension T decreases: this means that the value of the tension will be minimum in the extreme positions.

So the correct answer is D. None of the above