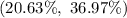Answer:
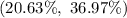
Explanation:
The confidence interval for population proportion(p) is given by :-
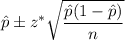 , where
, where
n= Sample size
z*= Critical z-value.
 = sample proportion.
= sample proportion.
Let p be the true proportion of all adults that have high blood pressure.
As per given , we have
n= 118
Number of adults found to have high blood pressure =34
Then,
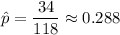
Critical z-value for 95% confidence interval : z* = 1.96
Now , the 95% confidence interval for population proportion will be :

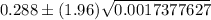
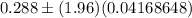
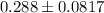
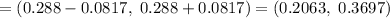
In percentage , this would be

Hence, the 95% confidence interval for the true percentage of all adults that have high blood pressure =